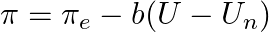Math and the Phillips Curve

Well, you've been warned

In our last article, we introduced the Phillips curve from a rather abstract, conceptual standpoint. With the inflation-unemployment relationship being well established in both the long and short run, it’s time to take things to the next level. Today, we’re going to go over the mathematics grounding the Phillips curve. 

The original 

William Phillips came up with the first Phillips curve equation (yes, there are multiple) sometime after publishing his 1958 paper. It was a relatively simple formula, designed solely to quantify his findings in the relationship between wage inflation and unemployment.

The “g” operator can be thought of as the “percent growth rate” of whatever variable that follows. Hence, “gW” is the growth rate of nominal wages whereas “gW^T” represents the trend rate of growth of those wages, and “f(u)” is the unemployment rate. Translating this into plain terms, and it becomes fairly intuitive. The growth of nominal wages corresponds with the overall trend of that growth rate and falls with the unemployment rate – an inverse relationship between unemployment and wage growth.

During the 1970s, however, several economists pointed out a crucial detail that the first equation didn’t encapsulate; workers will try to keep up with inflation through demanding more wages, sometimes preemptively. Inflation expectations were left completely out of the equation (pun). Factoring this element in:

In this case, the λ represents the weight given to “P^ex”, the inflation expectation. It’s important to consider that people estimate inflation with varying degrees of certainty and attention (i.e. compare a very certain forecast of +10% inflation as opposed to an uncertain forecast of whether inflation will be 3.01% vs 3.02%). On that note, we can reasonably assume that the more weighting assigned to an inflation expectation, the more responsive people will be in how they negotiate wages. Thus, a larger λ means changes in wage inflation will be more sensitive to changes in inflation expectation.

This leads to another key idea: how inflation expectations impact not just wage growth but inflation as a whole. Put simply, if people anticipate goods to be more expensive in the future, they’re going to buy more things while everything’s still cheap. Increased spending, and we all know what that produces…more inflation! It’s almost a self-fulfilling prophecy, with the very anticipation of inflation causing inflation. 

But this wasn’t the only modification made. The unemployment function was expanded to incorporate the non-accelerating inflation rate of unemployment (NAIRU) or the “natural” rate of unemployment. Our previous article goes into greater detail on this, but the NAIRU is the unemployment rate when the labor market is in equilibrium and thus, the lowest level of unemployment before inflation starts to increase. 

U* is the natural rate of unemployment, whatever that may be at any given time. If the actual unemployment is below it, then inflation should increase. Why? Because unemployment is “too low” (i.e. lower than the NAIRU), tightening the labor markets as employers compete for workers. Low unemployment implies that a lot of people are already working and aren’t willing to work at a new firm. That new firm will therefore have to offer higher wages to attract employees. So not only do workers have more spending money (thereby increasing aggregate demand which then increases inflation), but companies may also have to raise their own prices as a result of having to pay more in wages.

Conversely, if unemployment is above the natural rate, then we have a surplus of available workers with reduced bargaining power. Wages go down, as do the firms’ costs of production (a worker’s salary is considered a cost of production) and the workers’ spending since they have less money, which then cools inflation. 

The New Classical version

Robert Lucas was an American economist that came up with, among other things, the Lucas aggregate supply function. This model shows how economic output is by and large determined by what firms and workers expect to happen in an economy. Unlike the Phillips curve, the Lucas model emphasizes how changes in output are caused by price level changes.

“Y” is the economy’s total output, “Yn” is the natural level of output (that is, the output level that can be sustained for a long time), “P” is the current price level (the average price of goods and services across the economy) and “Pe” is the expected price level. The constant “a” is always positive because it represents how responsiveness the economic output is to the price level, so if P > Pe, the term a(P - Pe) becomes positive. In other words, prices are higher and therefore the total quantity of goods and services supplied exceeds the natural level (because firms are incentivized to produce more since they can sell their products and/or services at higher prices).

But when P < Pe, the term a(P - Pe) becomes negative, reflecting the fact that prices are lower because the total quantity of goods and services supplied falls behind the natural level (firms have lessened incentives to produce when prices lower).

So, what does this have to do with the Phillips curve? Well, let’s first rearrange the equation to solve for the current price level:

Next, we need to replace the P and Pe variables with inflation and inflation expectations, respectively. We can get a rough estimation of these values like so:

Here the current price level subtracted by last year’s price level gives an approximate idea of the inflation rate, and same thing for the expected price level. Just to clarify, the 𝛑 symbol isn’t 3.1415926…. economists just decided to adopt the Greek letter for their own usage to represent inflation. Now plugging everything in:

Similar to the equation from earlier, “b” is a positive constant attached to the difference between unemployment (“U”) and the natural rate of unemployment (“Un”). But we’re not quite done yet. The final variable we’re gonna throw in, “v,” represents unexpected exogenous supply shocks, which are, as the name suggests, sudden events that greatly affect the availability of production goods such as oils or metals. Why would we want to account for this? These shocks can shift the short-run aggregate supply (SRAS) curve and hence impact the inflation-unemployment relationship; if the SRAS shifts right following an increase in productivity and/or a decrease in prices, unemployment and inflation will decrease, ceteris paribus, and vice versa. 

And voilia! The New Classical Phillips curve equation, developed through the aggregate supply function.

The New Keynesian version

Because of how much more dynamic this one is, the New Keynesian Phillips curve (NKPC) initially looks significantly more complex than the previous 2. While that’s true to a certain extent, it borrows from the New Classical emphasis on inflation expectations, while factoring in a few additional metrics. Here goes:

𝛑t is the inflation rate at time t, which is calculated with the following: 

• Households’ discount factor, which measures people’s preferences for present vs future consumption. Denoted by 𝛽, a value of 1 means the household values future consumption whereas a value of 0 means the household values present consumption

• Inflation expectation at time t, denoted by Et(𝛑t + 1)

• k, which measures the degree to which changes in firms’ costs are passed on to consumer through changes in prices (the technical term is sensitivity of inflation to real marginal cost)

• Output gap, which is the difference between the actual economic output and its potential level at time t, denoted by ỹt 

The k value is calculated like this:

Where: 

• α is the labor supply elasticity, or how sensitive the quantity of supplied labor is to changes in wages. A very elastic labor market, for example, would mean that workers would easily quit to find another job if their pay decreases by a slight amount

• σ is what’s called the intertemporal elasticity of substitution (IES): a measurement of how much an individual or household is willing to change their consumption over different time periods. If you were high IES, you’d be perfectly willing to change your spending patterns over the next month in response to, say, rising interest rates. On the other hand, if you were low IES, you wouldn’t care about how the rising rates would affect prices and so your spending would stay the same

• φ is the disutility of labor; the hidden costs of working. Think of factors such as physical/mental exertion, stress, lost leisure time, etc. These are all things that we are forgoing in order to work a job 

• ϵ is demand elasticity, that is, how sensitive people’s demand is to prices changes

The λ, in this case, still represents the weight of the k value but must be tailored somewhat to the situation:

The theta (θ) is price stickiness, which refers to prices’ resistance to change. Why would we need this for determining the k-value? Price stickiness affects how quickly firms can adjust their prices in response to changes in their costs. If prices weren’t sticky at all, the change in real marginal cost would be followed immediately by a proportional change in price. But because prices are often sticky in reality, firms take time to respond to cost changes (that is, if they respond at all). 

Now for the main takeaway from all this. Unlike the New Classical Phillips curve, the NKPC is centered around price stickiness and its role in determining inflation. Put simply, firms tend to keep their prices fixed for a given period of time (which is where IES comes into play) before updating them if they so choose. As such prices can be an inaccurate gauge for the economy’s immediate health. That’s the first point: price stickiness matters.

Secondly, the importance of the household discount factor. If households are more willing to adjust their consumption and labor supply (that is, how willing they are to work), they’ll be more likely to substitute present consumption for future consumption, which directly affects demand elasticity and thus, prices overall.

Additionally, the household discount factor speaks to the effectiveness of central bank monetary policy. A higher discount factor, meaning that households will think more about future inflation, should compel a central bank to be more hawkish in restoring inflation to stable levels. Remember, if people are constantly worrying about how high inflation is going to be in a year’s time, then they’ll make all their large purchases now while it’s still cheaper, further driving inflation.

Lastly, the output gap. Think of this as how inefficient an economy is. A positive output gap means firms have less pricing power because of the increased competition among labor and capital suppliers (as there is more supply than demand for labor and capital and hence, an excess of firms), therefore lowering inflation. But if the output gap is negative, then there’s more demand than supply and less competition among suppliers. This gives each individual firm more pricing power, which generally results in inflation.

Econ IRL

With all the long-standing hype surrounding AI and automotive technologies, sometimes you just have to wonder to yourself: but where are all the robots? Shouldn't they be walking among us on the streets at this point? This week’s paper, which is incidentally the first ever systematic factory-level data analysis on robot use in America, seeks to address that burning question.

The authors analyzed data from the US Census Bureau’s Annual Survey of Manufacturers, they found that robots are distributed in a very skewed manner, with some areas having more than anyone would expect. For example, the bottom 25% of states ranked by the size of the auto manufacturing sector had a robot use rate of 1%, whereas the top 25% of states (with the largest auto manufacturing sectors) had a robot use rate of 39%. 

The authors also find a positive correlation between union membership and the presence of robot integrators (third parties that help manufacturers adopt robots), but are unsure of the reason for that. Given the potential conflicts in interest, one would expect for these 2 metrics to be negatively correlated. One possible theory, however, is that the threat associated with losing your job to a robot isn't enough to make up for the realized benefits of working alongside more efficient machines. 

‘Till next time, 

SoBasically