Volatility
The wild financial rollercoaster
There’s no questioning the importance of volatility in the field of finance. From risk assessment to option pricing to portfolio management, the idea of tracking and measuring price fluctuation is an unavoidable aspect of financial economics. Our previous 2 articles investigated how volatility fits into option pricing, but we’re going to take a deeper dive into the underlying theory of this seemingly obvious concept. So yes, there’s going to be some math and stats in this piece, but it’s a comparatively shorter one that should begin to make sense in the context of constantly-changing prices.
Types of volatility
The precise definition of “volatility” in finance is how much a price varies over time, and there are 2 ways to construe this. The first is the actual volatility, that is, the observed price fluctuations that have occurred in the past. The other, arguably more eminent metric is the implied volatility; the market’s expectations of future price fluctuations. Implied volatility can be further broken down like so according to how it’s measured:
Historical implied volatility, observed through the asset’s historical prices
Current implied volatility, observed through the asset’s current prices
Future implied volatility, observed through the asset’s future prices
Regarding the future implied volatility, it’s important to keep in mind how it differs from implied volatility – future implied volatility is usually interpreted as a projection of volatility levels over a predefined time frame, whereas implied volatility is used more for assessing the market’s perception of volatility.
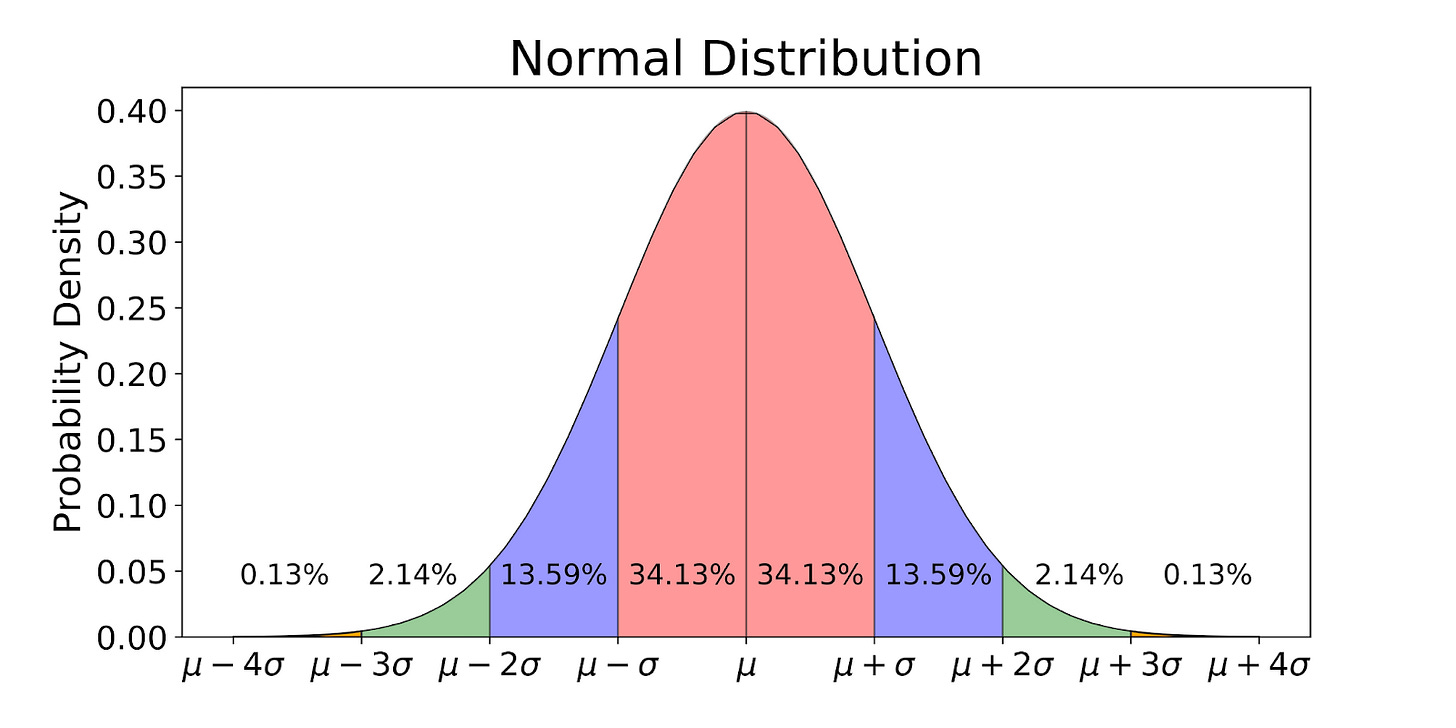
Another important note about volatility investors and economists usually assume financial prices to follow what’s called a Gaussian random walk. This mathematical model, as the name suggests, describes the movement of a variable whose changes follow a normal distribution (aka a Gaussian distribution), or what’s more commonly known as the bell curve.
Each step’s magnitude or size is determined by picking a random value from a normal distribution graph such as the one above. This means that the step can be either positive or negative, making the model perfect for prices in financial markets, which move up and down all the time. But where does this fit into price fluctuation?
The standard deviation (how spread out the values are in a dataset are relative to its mean) of the random walk process grows with the square root of time, meaning that the steps (prices) will gradually wander more and more from the mean (“initial price”) as time goes on. And of course they do; even a day’s worth of market dynamics, sudden events, and new information is enough to shift prices one way or the other, so it only follows that this effect will grow over several days.
But why the square root of time? Why doesn’t volatility increase linearly with time? Think of standard deviation as the average size of the random steps. Because some steps are negative and positive, taking their mean will cancel out some of them so to speak (think about how averages are calculated). As such, the steps’ standard deviation must increase at a rate slower than time, as every positive step will likely, to a certain extent, be countered with a negative step. This phenomenon, creatively called the “square root of time rule,” is why stock prices (usually) don’t double or halve in price after 2 days.
The math
Before getting to the official formula, we must first understand logarithmic returns - the relative change in value of an investment over a specific time period.
“Pf” is the final stock price, “Pi” is the initial stock price, and “ln” is the natural logarithm. For those of you who may not be familiar, this is a function that calculates the exponent needed to obtain a specific value when using the base “e” – Euler’s number. In the context of finance, this oddly important number represents the theoretical rate of return that an investment would receive if it were infinitely compounded in a given period of time.
The natural logarithm of the final value/initial value ratio yields the investment’s logarithmic return. The main advantage of using log returns as opposed to simple returns is that you can add them across time periods. Say a $50 share rises to $75 in Day 1 but drops back to $50 the following day. A simple return analysis would suggest a 50% increase the first day and a -33.33% decrease the second day – an average return of roughly 8.5% even though you didn’t actually gain any money.
But if we were to add up the log returns, you get an accurate picture of how much money was made.
Now that log returns have been cleared up, the grande finale. An asset’s volatility can be expressed like so:
Volatility is represented by the standard deviation of the asset’s logarithmic returns, denoted with Sigma-T in this equation, with T being the time period for which the volatility is being calculated. The second sigma is the standard deviation of the log returns for each second-order time interval. So if we wanted the volatility across a year, then the second sigma would be the asset’s standard deviation of daily log returns.
Econ IRL
President Biden’s Inflation Reduction Act has drawn both support and criticism since its proposition. While its name suggests an attempt to ease the impact of rising prices on households, the legislature is in fact far more extensive and far-reaching and covers several areas of government reform. Among these goals is to increase compliance with American taxes through modernizing the tax system. This week’s paper looks over the effectiveness of these efforts.
The researchers estimate a $560 billion gain in new taxes as a result of the Inflation Reduction Act. This growth, however, will take several years to materialize as the IRS’s fundamental problem is a deficiency in their auditing department (which is necessary for taxing corporations, high-earners, etc). As such, the investment will likely go to teams of lawyers and accountants to regularly pour over thousands of pages of earnings and figure out how much they’re owed – and it will take years for these teams to become fully productive.
‘Till next time
SoBasically